-
 |
 CHAPITRE 1
CHAPITRE 1
|
-
- auteur: Philippe
Moreau (U.P.J.V.)
UN LANGAGE ALGORITHMIQUE
Après une brève introduction, nous définirons les
objets utilisables par la machine: les objets existants appelés constantes
(1)types de bases - constantes)
et ceux permettant un stockage temporaire appelés variables (2)variables et déclarations).
Puis, seront définis, les opérateurs pouvant agir sur ces
objets (3)opérateurs et
fonctions) ce qui permettra de construire des objets plus complexes
(4)les expressions) que
l'on pourra stockés en mémoire en utilisant les variables
(5)l'affectation). On introduira
également la notion de variables dimensionnées (6)variables indicées ou tableaux) permettant
le stockage de plusieurs informations référencées par
un même label.
On présentera ensuite les instructions qui permettent d'établir
un dialogue entre le programme et l'utilisateur (7)afficher-lire)
Puis les structures de contrôle permettant l'écriture de
programme (8)si..alors..sinon
et 9)les boucles)
Enfin une notion essentielle qui permet, entre autre, de structurer un
programme (10)les procédures
et fonctions)
-
- Vous trouverez également quatre séries d'EXERCICES:
- - Une série concernant les sections de 1 à 5 et également
la section 7 (Série 1-5.7)
- - Une série concernant la section 8 (Série
8)
- - Une série concernant les sections de 6 et 9 (Série
6.9)
- - Et une série concernant la section10 (Série
10)
- Ces exercices sont également accessibles à la fin de
la dernière section concernée.
-
- Introduction:
- Le but, ici, n'est pas de définir un nouveau langage muni de
ses contraintes de syntaxes et de sa panoplie d'instructions et fonctions,
mais au contraire de se munir d'un langage simple à utiliser, facilement
compréhensible et qui de plus permettra une "traduction"
aisée dans un langage de programmation (On remarquera que ce langage
est d'ailleurs assez proche des langages PASCAL et C). Ainsi, par exemple,
les mots clés seront en français et la syntaxe ne sera pas
trop rigoureuse.
- Toutefois ce langage devra répondre aux exigences suivantes:
- - il sera structuré
- - il sera puissant
- - il sera évolutif
1) types de base - constantes
Ce sont les objets que manipule un ordinateur: données numériques,
alphanumériques ou booléennes.
- - les entiers
- Ce sont tous les entiers relatifs
- Exemple: 1 5196 -487596 0
- Remarque: Dans le Langage Algorithmique (L.A.) on supposera
que les nombres entiers ne sont pas bornés.
-
- - les réels
- Ce sont tous les nombres réels
- Exemple: 1 51 0.2648 25.5E-10
18E20
- Remarque: De la même façon on supposera, dans le
L.A. que tous les réels, même irrationnels (exemple: , ÷2)
sont accessibles (sauf contre indication dans des cas spécifiques).
-
- - les booléens
- Ils sont au nombre de deux VRAI et FAUX
-
- - les caractères
- Ce sont tous les caractères connus
- Exemple: 'a' 'z' '0' 'ù'
':' '°' ' ' etc
-
- - les chaînes de caractères (chaînes)
- Ce sont des séquences obtenues en concaténant plusieurs
caractères
- Exemple: 'bonsoir' 'il fait froid' '254.25' 'j''imagine'
- Remarque: les constantes caractères ainsi que les constantes
chaînes apparaîtront entres apostrophes.
- La constante apostrophe sera représentée par une double
apostrophe.
2) variables et déclarations
Au cours d'un traitement, il est nécessaire de pouvoir conserver
certaines données afin de les exploiter ultérieurement. Pour
cela on utilise des variables (emplacements mémoire) dans lesquelles
l'ordinateur viendra stocker les données au cours du traitement.
- Une variable est représentée par un identificateur (ou
nom de la variable) qui est un mot répondant aux exigences suivantes:
- - il est composé de lettres et de chiffres
- - il commence par une lettre
- Exemple: TOTO TITI fich rac min FLAG
- Contre exemple: GK+ F- 2xlp
-
- Remarques:
- - il est fortement conseillé d'utiliser des identificateurs
significatifs.
- - Une variable (et donc son identificateur associé) est typée:
elle prendra soit des valeurs entières, soit des valeurs réelles,
etc
- Le type de la variable est défini lors de la déclaration
de celle-ci.
-
- Déclaration
- Toute variable doit être déclarée. Ceci se fait,
avant l'utilisation de celle-ci, de la façon suivante:
- Type de variable liste
d'identificateurs
-
- Exemple:
- ENTIER i , j , k
- REEL min , x , rac
- BOOLEEN flag , drap
3) opérateurs et fonctions
- - les opérateurs arithmétiques
| + (addition) |
* (multiplication) |
% (division entière 17%3 donne 5) |
| - (soustraction) |
/ (division) |
^ (exponentiation) |
-
- - les opérateurs logiques
- ET OU NON
- Rappels:
- - tables de vérités des fonctions logiques

-
- - les opérateurs relationnels
| = (égal) |
< (inférieur) |
<= (inférieur ou égal) |
| <> (différent) |
> (supérieur) |
>= (supérieur ou égal) |
-
- - l'opérateur concaténation
- + (réalisant la concaténation de deux chaînes de
caractères)
-
-
- - les fonctions numériques
- Exemples:
- cos (cosinus) sin (sinus) abs (valeur absolue) rac (racine carrée)
etc
- Remarque: On utilisera toutes les fonctions qui seront nécessaires.
Il conviendra de définir celles-ci si le langage de programmation
utilisé ne les possède pas.
-
- - les fonctions sur les chaînes
- Celles-ci seront également définies lorsque le besoin
s'en fera sentir. A titre d'exemple la fonction longueur pourra
être définie comme donnant le nombre de caractères
contenus dans une chaîne de caractères.
4) les expressions
- Moyen d'obtenir une valeur en utilisant les constantes, variables,
opérateurs et fonctions.
- Exemples:
- 'soir'
- x
- 25
- 15 + 18 * (rac(f + 4 * x) - cos(3 * pi / x)) ^ 2
- NOM + 's'
- Important:Priorité des opérateurs arithmétiques
dans une expression: l'application des différents opérateurs
se fait dans l'ordre suivant: le -(unaire), ^ , * / et %, + et -
- les opérateurs *, /, % ont la même priorité ainsi
que les opérateurs + et -. L'application de ceux-ci se fera donc
en procédant à une lecture classique (de gauche à
droite).
- Exemple: l'écriture - 2 + 4 * x ^ 2 / y * x + 2
- correspond à l'expression:

5) l'affectation
- notée <-- elle permet d'affecter, à une variable,
une nouvelle valeur.
-
- Syntaxe: Identificateur <-- expression
- Exemples:
- I <-- 5
- nom <-- nom + prenom
- min <-- 4 * pi - cos(x + y)
- flag <-- VRAI
- Remarque: La valeur représentée par l'expression
doit être du même type que la variable. Toutefois si le résultat
de l'expression est réel et la variable entière, on admettra
que celle-ci peut recevoir la valeur calculée tronquée à
la partie entière.
6) variables indicées
ou tableaux
- Dans certains cas, il est nécessaire de regrouper plusieurs
données sous un même label (identificateur), on réserve
alors un certain nombre de 'cases' en mémoire pour venir y stocker
ces différentes données. L'ensemble de ces 'cases' en mémoire
est alors appelé tableau.
- Un tableau est donc référencé par un identificateur.
De plus il faut pouvoir accéder à une 'case' de celui-ci;
pour cela on utilise la notation suivante:
- Identificateur [ N ] qui fait référence à
la Nième case du tableau désigné par identificateur.
-
- Exemple: Considérons un tableau T d'entiers.
- T [ 5 ] <-- 25 affecte la valeur 25 à la 5ème
case du tableau T.
- x <-- T [ 4 ] met dans la variable x le contenu de la 4ème
case de T.
- Les tableaux peuvent également posséder plusieurs dimensions.
C'est le cas lorsque l'on veut traiter un problème faisant appel
aux matrices. Ainsi:
- Exemple:
- MAT [ i , j ] fera référence à la 'case' située
à l'intersection de la ième ligne et de la jème colonne.
- Remarque: Le ou les numéros de la 'case' spécifiée
porte également le nom d'indice (indice de ligne, indice
de colonne pour un tableau à deux dimensions).
-
- Déclarations
- On visualisera les variables indicées par le fait qu'elles seront
suivies de crochets ouvrant et fermant.
- Les tableaux des exemples seront déclarés sous la forme
suivante:
- ENTIER T [ ] , MAT [ ]
7) afficher, lire
- Au cours de l'exécution d'un programme, il est indispensable
de pouvoir communiquer avec l'ordinateur. Cela est rendu possible grâce
à l'emploi des instructions afficher et lire.
-
- afficher
-
- Syntaxe: afficher liste d'expressions
-
- permet d'afficher les différents résultats des calculs
réalisés par les expressions.
- Remarques:
- - On ne se soucis pas de la forme d'affichage.
- - On pourra également afficher des tableaux (exemple: afficher
T [ ]) sans se préoccuper de la présentation.
- - Il est souvent utile (voir nécessaire) d'afficher des messages
lors de l'exécution d'un programme pour permettre l'interprétation
des résultats affichés.
- Exemples: afficher 'le montant hors taxe est:' , THT
- afficher 'le plus grand est=' , max
- afficher 'la racine carrée de ' , x , ' est ' , rac(x)
-
- lire
-
- Syntaxe: lire liste de variables
-
- permet à l'utilisateur de rentrer des données.
- Exemple: lire x , y
- afficher x + y
- Remarque: Dans le cas où la lecture d'un tableau n'est
pas une contrainte à étudier, on pourra se contenter d'écrire
"lire T [ ]" (si T est le tableau à entrer).
-
EXERCICES d'application sur les sections de 1 à 5 et également
la section 7
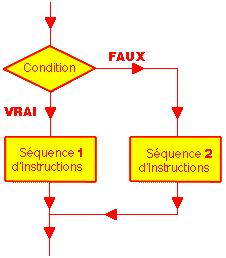
8) Si alors sinon
- Structure de contrôle permettant de rendre conditionnelle l'exécution
de séquences d'instructions.
-
- Syntaxe:
- si condition alors
- |
- | séquence 1 d'instructions
- |
- sinon
- |
- | séquence 2 d'instructions
- |
- finsi
-
- Si la condition est vraie alors le programme exécute la séquence1
d'instructions puis il se poursuit après l'instruction finsi, sinon
(condition fausse) il exécute la séquence2 d'instructions.
Le fonctionnement de cette structure peut se visualiser par le schéma
suivant:
- Remarque: Dans certain cas la séquence2 d'instructions
n'existe pas; la syntaxe et le schéma sont alors réduits
à la forme suivante:
-
- si condition alors
- |
- | séquence 1 d'instructions
- |
- finsi
|
 |
- Exemple:
- - calcul du minimum de deux nombres entiers
- ENTIER A , B , MIN
- AFFICHER 'donnez deux entiers'
- LIRE A , B
- SI A < B ALORS
- MIN <-- A
- SINON
- MIN <-- B
- FINSI
- AFFICHER 'le minimum de ' , A , ' et de ' , B , ' est ' , MIN
-
- ce qui peut s'écrire:
- ENTIER A , B , MIN
- AFFICHER 'donnez deux entiers'
- LIRE A , B
- MIN <-- B
- SI A < B ALORS
- MIN <-- A
- FINSI
- AFFICHER 'le minimum de ' , A , ' et de ' , B , ' est ' , MIN
-
EXERCICES d'application sur la section 8
9) les boucles
- Il arrive fréquemment qu'un même type d'actions (suite
d'instructions) se répète plusieurs fois dans un programme
de façon consécutive. On a alors la possibilité et
souvent l'obligation d'utiliser une structure dite de boucle.
-
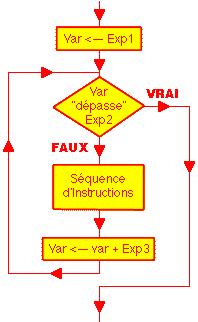
- - les boucles définies
-
- Ces boucles sont appelées "définies" car c'est
le programmeur qui spécifie le nombre de fois que la boucle doit
s'exécuter.
-
- Syntaxe:
- pour variable allant de expression1 jusqu'à
expression2 avec un pas de expression3 faire
- |
- | séquence d'instructions
- |
- finpour
-
- Remarque: La variable est appelée variable de contrôle
ou indice de boucle.
-
-
-
- A l'origine la variable de contrôle prend comme valeur, la valeur
décrite par expression1.
-
- Si la valeur de l'indice n'a pas "dépassé"
la valeur décrite par expression2 alors la séquence d'instructions
est exécutée.
-
- Puis l'indice est incrémenté de la valeur décrite
par expression3 et est à nouveau testé avec expression2.
-
-
- Si la valeur de l'indice a "dépassé" la valeur
décrite par expression2 alors le programme continu son exécution
après l'instruction finpour.
|
|
- Remarques:
- - l'indice ne peut en aucun cas être modifié à
l'intérieur de la boucle.
- - le test est fait en début de boucle.
- - on simplifie l'écriture par:
- pour variable <-- expression1 jusqu'à
expression2 pas expression3 faire
- |
- | séquence d'instructions
- |
- finpour
- - fréquemment le pas prend la valeur 1. On écrira alors:
- pour variable <-- expression1 jusqu'à
expression2
- |
- | séquence d'instructions
- |
- finpour
-
- Exemples:
- - Somme des N premiers entiers naturels
- ENTIER I , N , S
- AFFICHER 'entrez une valeur entière'
- LIRE N
- S <-- 0
- POUR I <-- 1 JUSQU'A N FAIRE
- S <-- S + I
- FINPOUR
- AFFICHER 'la somme des ' , N , ' premiers entiers est ' , S
- vous pouvez voir un exemple d'exécution
de ce programme
-
- - lecture des valeurs d'un tableau de données entrées
par l'utilisateur ce qui peut s'écrire:
- LIRE T [ ]
- peut aussi s'écrire:
- POUR I <-- 1 JUSQU'A N FAIRE
- AFFICHER 'entrez la ' , I , ' ème valeur: ' ; LIRE T [ I ]
- FINPOUR
- Où N est le nombre d'éléments du tableau.
- les boucles indéfinies
- Ici le programmeur ne sait pas combien de fois doit s'exécuter
la suite d'instruction contenue dans la boucle et d'une manière
générale, ces boucles se répètent jusqu'à
ce qu'un certain événement se produise. Elles sont de deux
types: les boucles "tant que" et "répète
jusqu'à".
-
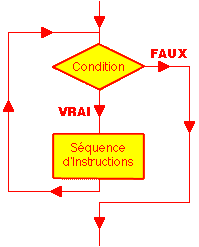
- la boucle tant que
-
- Syntaxe et schéma de fonctionnement:
-
- tant que condition
faire
- |
- | séquence d'instructions
- |
- fintantque
-
-
-
- Remarques:
- - fintantque sera souvent abrégé fintq ou même
ftq.
- - le test est fait en début de boucle (on peut donc simuler
une boucle "pour" à l'aide d'une boucle "tant que").
|
|
-
- Exemple: calcul de A modulo B (reste de la division, entière
de A par B).
- ENTIER A , B
- AFFICHER 'calcul de A modulo B (A et B positifs)'
- AFFICHER 'donnez deux entiers positifs'
- LIRE A , B
- AFFICHER A , ' modulo ' , B , ' = '
- TANT QUE A >= B FAIRE
- A <-- A - B
- FINTANTQUE
- AFFICHER A
- vous pouvez voir un exemple d'exécution
de ce programme
-
-
- la boucle repete jusqu'à
-
- Syntaxe et schéma de fonctionnement:
-
- repete
- |
- | séquence d'instructions
- |
- jusqu'à condition
-
-
-
-
- Remarques:
- - le test de sortie est fait en fin de boucle.
- - la séquence d'instructions s'exécute donc au moins
une fois.
|

|
-
- Exemple: contrôle de l'entrée d'un entier par l'utilisateur.
- REPETE
- AFFICHER 'donnez un entier ' ; LIRE N
- JUSQU'A N = ent(N)
-
- où ent(N) désigne la partie entière de N
- vous pouvez voir un exemple d'exécution
de ce morceau de programme
IMPORTANT: Des Conseils
pour écrire une boucle
-
-
EXERCICES d'application sur les sections 6 et 9
10) procédures et fonctions
- La notion de procédure est une notion fondamentale qui permet
de:
- - structurer un programme
- - diviser les difficultés
- - accroître la lisibilité d'un programme
- - éviter les répétitions
- -constituer des bibliothèques
- Ainsi dès qu'une tâche est cernée et définie
il est utile et souvent indispensable de faire une procédure reflétant
cette tâche.
-
- Exemple:
- - affichage d'une matrice
- - tracé d'une ligne
- - calcul d'une équation
- - etc
- les fonctions
- portion de programme destinée à produire un résultat
utilisable par la partie de programme appelante.
-
- Syntaxe:
- fonction type de base
nom de la fonction(liste de paramètres)
- déclaration des paramètres
- déclaration des variables internes à
la fonction
- |
- | corps de la fonction
- |
- | résultat (résultat
du calcul effectué par la fonction)
- Exemple: fonction calculant le PGCD (algorithme vu dans un exemple de boucle)
- FONCTION ENTIERE PGCD(A , B)
- DONNEES ENTIERES A , B
- ENTIER R
- TANT QUE B <> 0 FAIRE
- R <-- A - (A % B) * B
- A <-- B
- B <-- R
- FINTANTQUE
- RESULTAT (A)
-
- Remarques:
- - la liste de paramètres se présente sous la forme d'une
liste de variables dont les noms sont propre à la fonction.
- - si besoin est, on peut également déclarer des variables
internes à la fonction, là encore les noms de ces variables
sont propre à la fonction.
- - la communication entre le programme (ou portion de programme) appelant
et la fonction se fait grâce aux paramètres et au "résultat".
-
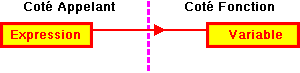
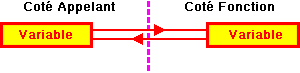
- IDEE: On peut se représenter le passage de la portion
de programme appelante à la fonction (et de la fonction au programme
appelant) comme une sorte de frontière (virtuelle) par laquelle
passent des informations qui obéissent à certaines règles.
Ainsi certaines informations peuvent passer de la partie appelante vers
la fonction, alors que d'autres passent de la fonction au programme appelant.
Ceci dépendra du type choisi, lors de la déclaration des
paramètres.
-
-
- On distingue trois types de paramètres:
-
- - les données:
-
- la fonction utilise la valeur du paramètre mais n'apporte aucune
modification du coté appelant.
- coté appelant, le paramètre peut être sous la forme
d'une expression.
-
-
- - les données résultats
-
- la fonction utilise la valeur du paramètre mais, si celui-ci
est modifié dans la fonction, cette modification est reportée
du coté appelant.
- coté appelant, le paramètre doit être une variable.
-
- - les résultats
-
- la fonction n'utilise pas la valeur du paramètre mais celui-ci
sera affecté dans la fonction et cette valeur sera retransmise du
coté appelant.
- coté appelant, le paramètre doit être une variable.
-

-
- - la sortie de la fonction est assurée par l'instruction résultat qui a pour effet de renvoyer le résultat
d'un calcul effectué par la fonction.
- Cette instruction peut être placée à un endroit
quelconque de la fonction (il faudra toutefois s'assurer que l'instruction
est utilisée pour la sortie de fonction). L'instruction "résultat"
peut également apparaître plusieurs fois à l'intérieur
d'une même fonction.

-
- Utilisation d'une fonction: Une fonction s'utilise telle une
valeur
- Exemples:
- P <-- PGCD(A , B)
- Q <-- PGCD(A , PGCD(B , C + 5) + 1)
-
- - il semble évident que la position des expressions et variables
au moment de l'appel conditionne l'interprétation de celles-ci à
l'intérieure de la fonction.
-

- les procédures
- portion de programme destinée à réaliser un traitement
utilisable par la partie de programme appelante.
-
- Syntaxe:
- procédure nom de la procédure
(liste de paramètres)
- déclaration des paramètres
- déclaration des variables internes à
la procédure
- |
- | corps de la procédure
- |
- retour
-
- Exemple: procédure calculant le PGCD
- PROCEDURE PGCD(A , B , C)
- DONNEES ENTIERES A , B
- RESULTAT C
- ENTIER R
- TANT QUE B <> 0 FAIRE
- R <-- A - (A % B) * B
- A <-- B
- B <-- R
- FINTANTQUE
- C <-- A
- RETOUR
-
-
- Remarques:
- - la procédure diffère de la fonction, essentiellement
par le fait qu'elle ne produit pas de résultat. Sur l'exemple on
s'apperçoit que ce n'est pas réellement un handicap et que
l'on pourrait se contenter que de le notion de procédure.
-
- - de même que pour la fonction, bien que souvent placée
en fin, l'instruction retour peut apparaître plusieurs fois
dans la procédure.
-
- - la procédure s'utilise telle qu'une instruction
- Exemple: PGCD(I , J , K) ; AFFICHER ' le PGCD de ' , I , ' et de '
, J , ' est: ' , K
Une Notion Importante: La Récursivité
La récursivité se constate lorsqu'une
procédure (ou fonction) fait appel à elle-même. Mais
la notion de récursivité va bien au delà de cette constatation.
Ainsi, pour un problème donné; la façon
de concevoir sa résolution peut passer par une solution itérative
ou bien par une solution récursive. Pour aboutir à une solution
récursive il faut pouvoir énoncer la résolution d'un
problème P en évoquant, dans l'algorithme mis en oeuvre, la
résolution du même problème P (mais avec des données
différentes).
Exemple:
Reprenons le problème du calcul du PGCD de deux nombres entiers
A et B (A > B >=0). La solution (commentée dans l'exemple d'écriture d'une boucle) tient
compte de l'énoncé de l'algorithme en langage naturel et
aboutie, logiquement, à l'écriture d'un algorithme itératif;
et donc à la fonction suivante:
- FONCTION ENTIERE PGCD(A , B)
- DONNEES ENTIERES A , B
- ENTIER R
- TANT QUE B <> 0 FAIRE
- R <-- A - (A % B) * B
- A <-- B
- B <-- R
- FINTANTQUE
- RESULTAT (A)
-
Mais on aurait pu énoncer l'algorithme de calcul,
de la façon suivante (algorithme récursif):
- Après de première division
- On peut constater que: Le PGCD de A et de B est identique à
celui de B et de R
PGCD de A et B = PGCD de B et R
Ce qui induit alors la notion de récursivité (le calcul
d'un PGCD revient à calculer un autre PGCD). On en déduit
alors l'écriture de la fonction suivante:
- FONCTION ENTIERE PGCD(A , B)
- DONNEES ENTIERES A , B
- ENTIER R
- SI B <> 0 ALORS
- R <-- A - (A % B) * B
- RESULTAT ( PGCD ( B , R ) )
- SINON
- RESULTAT ( A )
- FINSI
-
-
- Remarque: Lors de l'écriture d'une procédure
récursive, on peut transposer les conseils
d'écriture d'une boucle.
- Les problèmes liés à l'initialisation étant
souvent résolus par l'écriture de l'appel de la procédure
(ou fonction).
-
-
EXERCICES d'application sur les sections 6 et 9
Auteur: Philippe Moreau
(U.P.J.V.)








