Rappels de numération
Page réalisée par:
Philippe Moreau
UPJV

Après un petit rappel sur l'écriture d'un nombre dans une base quelconque, on passera en revue les différents systèmes utilisés en Informatique, puis on s'intéressera aux méthodes de conversions des nombres entiers(calcul de l'expression, divisions successives, utilisations de table de puissances ou table de correspondance). Enfin on terminera par des additifs concernant le cas des Fractionnaires

Ecriture d'un nombre dans une base quelconque

Un système de numération est un ensemble composé d'un nombre B (appelé base) et d'un ensemble C = { a , b , c , d , ....} dont les éléments sont appelés des chiffres.

L'écriture d'un nombre X = xnxn-1. . . x2x1x0, x-1x-2. . . x-(p-1)x-p dans ce système s'interprète alors en réalisant le calcul suivant:


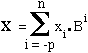
X = xnBn + xn-1Bn-1 + . . . + x2 B2 + x1B1 + x0B0 + x-1B-1 + x-2B-2 + . . . + x-(p-1)B-(p-1) + x-pB-p

définitions: en considérant la partie entière de X, xn est appelé le chiffre de poids fort ( et par extention xnxn-1 sont les chiffres de poids fort) alors que x0 est appelé le chiffre de poids faible ( et par extention x2x1x0sont les chiffres de poids faible).

Les systèmes de numérations utilisés en informatique

En informatique, on travaille essentiellement avec trois systèmes de numération (un quatrième système de numération est parfois rencontré).

1 - Tout d'abord, le système le plus fréquemment utilisé (car l'informatique "ce sont" les machines, mais surtout les hommes qui les utilisent) est le système décimal (dit à base 10).

On a alors B = 10 et C = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }
le nombre X = 2589 s'interprète comme étant le résultat du calcul:
X = 2.103 + 5.102 + 8.101 + 9.100
Remarque: par soucis de simplification, pour la compréhension, les puissances de la base seront toujours mentionnées dans la base dix.

2 - La représentation des informations en machines reposant sur le principe du "tout ou rien", cela nous conduit de façon naturel à évoquer le système binaire (dit à base 2).

On a alors B = 2 et C = { 0 , 1 }
et le nombre X = 1011 s'interprète comme étant le résultat du calcul:
X = 1.23 + 0.22 + 1.21 + 1.20
Remarque: toujours par soucis de simplification la base utilisée sera écrite dans la base dix.

3 - Pour résoudre les problèmes dûs à l'affuence d'informations de type "0 ou 1" (grande quantité de chiffres à "saisir" ou à "lire") on a été amené à utiliser le système hexadécimal (dit à base 16).

On a alors B = 16 et l'ensemble des chiffres utilisés en base dix est complété par les six premières lettres de l'alphabet
C = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , A , B , C , D , E , F }
ainsi le nombre X = A7C5 s'interprète par le calcul:
X = A.163 + 7.162 + C.161 + 5.160

4 - L'utilisation du système octal (dit à base 8) repose sur la même idée que pour l'hexadécimal (regrouper des informations "0 ou1").

dans ce cas B = 8 et C = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 }
et le nombre X = 5071 s'interprète par:
X = 5.83 + 0.82 + 7.81 + 1.80
Conversion d'un nombre
Cas des entiers

Problème: On considère un nombre entier NB écrit dans une base B et on souhaite trouver l'écriture de ce nombre dans une base B'.

Pour cela il existe quatre méthodes classiques permettant cette opération (appelée conversion). Les deux premières méthodes peuvent être appliquées pour des bases B et B' quelconques, alors que les deux dernières méthodes s'appliquent essentiellement dans des cas particuliers.

1ère Méthode: Le calcul de l'expression représentant le nombre

Principe: Cette première méthode consiste à effectuer le calcul de l'expression qui définit le nombre. Ainsi, si le nombre NB s'écrit NB=abcd dans la base B on effectuera le calcul de l'expression:

a . B3 + b . B2 + c . B1 + d . B0      pour trouver l'écriture de NB dans la base B'.

Remarques:

- tous les calculs (additions, multiplications, exponentiation) sont effectués dans la base B'.

- en conséquence, cette méthode sera surtout utilisée (par l'être humain) lorsque la base B' = 10.

Exemple: on considère le nombre NB = 1 1 1 0 1 0 1 1 écrit dans la base 2 que l'on veut écrire dans la base 10. On effectue alors, dans la base 10, le calcul suivant:

1.27 + 1.26 + 1.25 + 0.24 + 1.23 + 0.22 + 1.21 + 1.20

= 128 + 64 + 32 + 0 + 8 + 0 + 2 + 1

= 235

Notation: On écrira alors:

(1 1 1 0 1 0 1 1)2 = (2 3 5)10

Remarque: A titre d'exemple nous allons écrire les opérations à réaliser si nous avions à convertir le nombre NB = 235 (écrit dans la base 10) dans la base 2. On réaliserait alors le calcul suivant:

1 0 . 1 0 1 0 10 + 1 1 . 1 0 1 0 1 + 1 0 1 . 1 0 1 0 0

= 1 1 0 0 1 0 0 0 + 1 1 1 1 0 + 1 0 1

= 1 1 1 0 1 0 1 1

2ème Méthode: La méthode des divisions successives

Principe: Cette deuxième méthode consiste à effectuer des divisions successives entières du nombre NB = abcd (écrit dans la base B) jusqu'à l'obtention d'un quotient nul. Au cours de ces divisions on note les différents restes et ceux-ci permettront l'écriture du nombre dans la nouvelle base B'. Voici schématiquement les opérations à réaliser:

On pourra alors écrire:

(a b c d)B = (Rn+1 Rn . . . R2 R1)B'

Remarques:

- tous les calculs (divisions donc soustractions, multiplications) sont effectués dans la base B.

- en conséquence, cette méthode sera surtout utilisée (par l'être humain) lorsque la base B = 10.

Exemple: on considère le nombre NB = 2 3 5 écrit dans la base 10 que l'on veut convertir dans la base 2. On effectue alors, dans la base 10, les calculs suivants:

Remarque: toujours à titre d'exemple (dans le but de montrer que cette méthode peut être appliquée pour des bases quelconques) nous aurions pu convertir le nombre NB = 1 1 1 0 1 0 1 1 (écrit dans la base 2) dans la base 10, en réalisant les divisions suivantes (en base 2):

3ème Méthode: (cas particulier) utilisation d'une table des puissances de 2 pour une conversion de la base 10 vers la base 2.

Principe: On commence par dresser une table des puissances de 2. Puis, considérant le nombre NB (écrit dans la base 10):
  1. On recherche, dans la table, la plus grande puissance de 2 inférieure ou égale au nombre à convertir.
  2. On note alors son existence.
  3. On soustrait cette puissance du nombre à convertir.
  4. Puis on convertit le reste issu de cette soustraction (si celui-ci est différent de 0).

Exemple: on désire convertir le nombre NB = 2 3 5 écrit dans la base 10 dans la base 2. Dans un premier temps on construit la table suivante:

20 = 1 25 = 32 210 = 1024
21 = 2 26 = 64 211 = 2048
22 = 4 27 = 128 212 = 4096
23 = 8 28 = 256 213 = 8192
24 = 16 29 = 512 214 = 16384

  1. on trouve 128 (= 27)
  2. cette étape est très importante (surtout la première fois) car elle permet de terminer le nombre de chiffres dans l'écriture du nombre. En effet, cette méthode consistant à rechercher la présence des 1 dans l'écriture binaire du nombre, il est nécessaire de noter à ce moment les emplacements où se positionneront des 0.
    On sait alors que le nombre s'écrit avec 8 chiffres (le premier 1 étant placé).
         le nombre converti s'écrira: 1 . . . . . . .
  3. on réalise la soustraction: 2 3 5 - 1 2 8 = 1 0 7
  4. a) b) c)
    64 (= 26) 1 1 . . . . . . 1 0 7 - 6 4 = 4 3
    32 (= 25) 1 1 1 . . . . . 4 3 - 32 = 11
    8 (= 23) 1 1 1 . 1 . . . 11 - 8 = 3
    2 (= 21) 1 1 1 . 1 . 1 . 3 - 2 = 1
    1 (= 20) 1 1 1 . 1 . 1 1 1 - 1 = 0

il reste alors à compléter l'écriture: en ajoutant des 0 dans les emplacements libres pour obtenir le résultat escompté:

1 1 1 0 1 0 1 1

(2 3 5)10 = (1 1 1 0 1 0 1 1)2

4ème Méthode: (cas particulier) une base s'écrit comme une puissance de l'autre B = B'n (ou Bn = B')

Principe: Dans ce cas (B = B'n), à un chiffre de la base B correspond un nombre de n chiffres dans la base B' (il existe une bijection entre les chiffres de B et les nombres de n chiffres écrits dans la base B'). Respectivement (cas où Bn = B'), à un ensemble de n chiffres dans l'écriture du nombre dans la base B', on associera un chiffre de la base B.

Remarques:

- Cette méthode de conversion est l'une des plus simple, puisqu'il s'agit simplement d'appliquer le principe du codage ou du décodage (utilisation d'une table de codes (ou correspondance)).

- Il suffit donc de calculer les tables de correspondances. Voici les deux tables de codages qui peuvent être utilisées dans les cas étudiés.

Table de correspondance
Hexadécimal - Binaire		   Table Octal - Binaire
00 0 0 08 1 0 0 0 0 0 0 0
10 0 0 191 0 0 1  10 0 1
20 0 1 0A1 0 1 0  20 1 0
30 0 1 1B1 0 1 1  30 1 1
40 1 0 0C1 1 0 0  41 0 0
50 1 0 1D1 1 0 1  51 0 1
60 1 1 0E1 1 1 0  61 1 0
70 1 1 1F1 1 1 1  71 1 1

Exemples:

Ex1: on veut convertir le nombre NB = 3 A 9 B , écrit dans la base 16, dans la base 2 (16 = 24). On remplace alors chacun des chiffres du nombre par le nombre de 4 chiffres correspondant et on obtient:

(3 A 9 B)16 = ( 1 1 1 0 1 0 1 0 0 1 1 0 1 1 ) 2

remarque: dans ce chapitre sur la numération les 0 qui précèdent l'écriture "significative" des nombres ne seront pas mentionnés.

Ex2: on veut convertir le nombre NB = 1 1 0 1 0 1 0 0 1 1 0 1 1 écrit dans la base 2 dans la base 8 (8 = 2 3). On remplace alors chaque blocs de 3 chiffres du nombre par le chiffre correspondant et on obtient (rmq: les blocs de 3 chiffres sont obtenus en découpant le nombre à partir de la droite c'est à dire dans le sens de lecture classique d'un nombre en vue de son interprétation (à partir des unités):

( 1 1 0 1 0 1 0 0 1 1 0 1 1 )2 = (1 5 2 3 3)8

Cas des fractionnaires

Problème: On considère cette fois des nombres qui ne sont pas entiers. Comme nous avons vu comment traiter la partie entière de ces nombres, on va s'intéresser à "la partie fractionnaire pure" de ces nombres c'est à dire considérer des nombres NB qui s'écrivent sous la forme:

NB = 0 , a b c d...   (où a, b, c, d sont des chiffres).

Revenons sur les quatre méthodes que nous venons d'étudier.

  1. la méthode 1 est utilisable telle qu'elle a été décrite. (comme on a vu que les calculs étaient fait dans la base d'arrivée, on l'utilisera surtout avec B'=10)
    exemple: avec B=2 et NB = 0 , 0 1 0 1 on fera le calcul suivant
    0.2-1 + 1.2-2 + 0.2-3 + 1.2-4 = 0,25 + 0,0625 = 0,3125
  2. la méthode 4 est aussi utilisable telle qu'elle a été décrite. (dans le cas de base s'écrivant comme une puissance de l'autre)
    exemple: avec B=2 et NB = 0 , 0 1 0 1 0 1 B'=16 on fera des regroupements de chiffres par paquets de 4 en partant de la virgule et en allant vers la droite (en prenant garde de compléter le dernier paquet obtenu par des zéros (si nécessaire)).
    Si le nombre NB est 0 , 1 1 0 0 0 1 on aura:
    0 , 1 1 0 0 0 1 --> 0, .1 1 0 0.0 1 0 0. --> 0 , C 4 en hexadécimal
  3. la méthode 3 est également utilisable telle qu'elle a été décrite (donc pour une conversion de la base 10 vers la base 2). Il suffit de compléter au préalable la table des puissances de 2, en y ajoutant les puissances négatives de 2.
    2-1= 0,5       2-2= 0,25       2-3= 0,125       2-4 = 0,0625       2-5 = 0,03125       etc...
    exemple 1: avec NB = 0 , 875 on fera les calculs suivants:
    • 0,875 - 0,5 (2-1) = 0,375 - 0,25 (2-2) = 0,125 - 0,125 (2-3) = 0 (fin de la conversion).
    • On note alors les puissances de 2 et on peut écrire: 0 , 875 = 0 , 1 1 1
    exemple 2: avec NB = 0 , 2 on commencera les calculs suivants:
    • 0,2 - 0,125 (2-3) = 0,075 - 0,0625 (2-4) = 0,0125 - 0,0078125 (2-7) = 0,0046875   etc ... (on peut démontrer que la conversion n'a pas de fin).
    • Avec les puissances de 2 trouvées on peut alors écrire: 0 , 2 = 0 , 0 0 1 1 0 0 1 ...
    • on constate que l'écriture n'étant pas déterminée il faudra trouver un mode d'arrêt ! ( définir la précision souhaitée)
  4. Pour la méthode 2 (qui permet la conversion des entiers par divisions successives) on va donner un complément qui permet de traiter la partie fractionnaire et qui a la particularité de donner une méthode permettant de trouver l'écriture exacte du nombre (même dans le cas d'une écriture "infinie")

Additif à la 2ème Méthode: Les multiplications successives

Principe: Comme dans le cas des divisions successives, le but est de retrouver les chiffres qui permettrons d'écrire le nombre dans la base B'. Pour cela on multiplie la partie fractionnaire pure par la base B. La partie entière de ce calcul correspond à un chiffre (dans la base B'). Puis on continue à multiplier la partie fractionnaire pure de ce nouveau résultat jusqu'à obtenir une partie fractionnaire nulle (et alors la conversion est terminée) ou en fonction de la précision souhaitée.

Exemple: Pour convertir le nombre 0,5625 (écrit dans la base 10) dans la base 2

Remarque:

- Avec cette méthode de conversion, on peut cette fois trouver une écriture du nombre dans la base B'. En effet, au cours des multiplications successives, dans le cas de nombre ne menant pas à un résultat nul, on finit par retrouver un résultat déjà obtenu. On pourra alors affirmer que les calculs générés entre les deux résultats vont se répéter, on donc que la séquence de chiffres générée va elle aussi se répéter indéfiniment pour écrire le nombre. On pourra donc indiquer que la séquence obtenue se réécrit un nombre infini de fois en utilisant la notation: (séquence)∞.

Remarque:

Les principes (algorithmes), appris dans les classes primaires, concernant les opérations: d'addition, de soustraction, de multiplication, de division, etc... s'appliquent (bien évidemment) sur les nombres écrits dans une base quelconque.