La fonction logarithme décimal
Introduction
Représentation graphique de la fonction
défine sur
Pour tout réel strictement positif , l'équation admet une unique solution, celle-ci est noté , et est appelée logarithme décimal de .
(cliquer sur l'étoile pour changer la valeur de .)1. Définition de la fonction logarithme décimal
Définition : D'après ce qui précède, on peut définir une nouvelle fonction, appelée logarithme décimal, qui à tout réel strictement positif
,
associe l'unique solution de l'équation
, notée
.
Cette fonction est donc définie sur ] 0;+ [ .
[ .
Cette fonction est donc définie sur ] 0;+
 [ .
[ .
Propriété
- Pour tout réel strictement positif, .
- et .
Essais sur quelques valeurs,
(cliquer sur l'étoile pour changer les données)
À l'aide de la calculatrice, vérifiez que vous trouvez bien les résultats ci-dessous:
log(600)=2.7781513
log(7.1)=0.85125835
log(1)= 0
À l'aide de la calculatrice, vérifiez que vous trouvez bien les résultats ci-dessous:
log(600)=2.7781513
log(7.1)=0.85125835
log(1)= 0
2. Propriétés algébriques
Propriété
Pour tous réels et ,et pour tout entier naturel , on a :
- Cette dernière formule reste valable pour tout réel ,
Exemples
(cliquer sur l'étoile pour changer les données) :
Pour et ,
(cliquer sur l'étoile pour changer les données) :
Pour et ,
3. Variations ,représentation graphique et signe.
Sens de variation
Théorème : la fonction logarithme décimal est strictement croissante sur ]0;+ [.
[.
 [.
[.
Représentation graphique de la fonction x
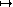 log(x) pour tout réel
log(x) pour tout réel
Théorème
Comme la fonction logarithme décimal est strictement croissante sur ]0;+ [ et que
, on en déduite que:
[ et que
, on en déduite que:
pour tout réel x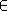 ]0;1[ et que
pour tout x
]0;1[ et que
pour tout x 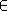 ]1;+
]1;+ [ .
[ .
Comme la fonction logarithme décimal est strictement croissante sur ]0;+
 [ et que
, on en déduite que:
[ et que
, on en déduite que:pour tout réel x
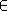 ]0;1[ et que
pour tout x
]0;1[ et que
pour tout x  ]1;+
]1;+ [ .
[ .